
Hence 3x + x + x 3 + x + x + 3 dx ln x3 + x + x c 5. Solution: Let f (x) x 3 + x + x + 3, then f (x) 3x + x +. So, we cn directly pply the logrithmic rule x x + 5 dx ln(x + 5) + c Exmple 5.9 Find 3x +x+ x 3 +x +x+3 dx. Logrithmic Rule dx lnx + c, x > x The more generl formul for logrithmic functions is given s f (x) dx ln f (x) + c, where f (x) > f (x) Exmple 5.8 Find x x +5 dx. We hve to rewrite the eqution in order to pply the formul e x dx ex dx e x dx ex + c where c is some constnt 5. Solution: Here we cn not directly pply the bove rule. Techniques of Integrtion 3 Exmple 5.7 Find e x dx. Solution: 3e 3x dx e 3x + c Any one cn get this soft-copy from Google site Exodus4Wisdom c Ntnel Nigussieģ 5. The more generl formul for n exponentil function is f (x)e f (x) dx e f (x) + c Exmple 5.6 Find 3e 3x dx. Exponentil Rule e x dx e x + c where c is ny constnt. Solution: (3x + 5x + )dx 3x dx + 5xdx + dx 3 x dx + 5 xdx + dx by constnt multiple rule 3x 3 + 5x + x + c by the power rule, where c is some constnt x x + x + c Notice tht in plce of seprte constnts of integrtion for ech of the three integrls, single constnt c ws dded t the end of (or c c + c + c 3 ). Sum-Difference Rule dx f (x)dx ± g(x) dx Exmple 5.5 Find (3x + 5x + )dx. Solution: x dx x+ + + c 3 x3 + c where c is some constnt. Power Rule x n dx n + xn+ + c for n Exmple 5.4 Find x dx. Constnt Multiple Rule c f (x)dx c f (x)dx where c is constnt. dx similr to the dx in the differentition opertor dx d, it shows tht the opertor hs to be performed with respect to the vribles x. f (x) is clled the integrnd (the function to be integrted). f (x)dx denotes integrtion of f (x) with respect to x. Integrl Nottion n elongted of S, is the integrl sign nd is derived from the first letter of the ltin word, Summ, which mens sum. It is clled indefinite integrl becuse it hs no definite numericl vlue. f (x)dx F(x)+c is clled the indefinite integrl of f (x) if nd only if F (x) f (x) for every x in the domin of f, c is clled the constnt integrtion. Any one cn get this soft-copy from Google site Exodus4Wisdom c Ntnel NigussieĢ Integrtion Definition 5. d dx F(x) d dx (x ) x f (x) Therefore, 3 x3 + 5 is n nti-derivtive of f (x) x. Solution: From the definition F(x) is n nti-derivtive of f (x) if nd only if F (x) f (x). Check whether the function F(x) x is n nti-derivtive of f (x) x or not.

Then F(x) is n ntiderivtives of f (x), becuse F (x) x + 3 f (x) for ll x. Let f be defined by f (x) x + 3 nd F by F(x) x + 3x. The process of finding nti-derivtives is clled nti-differentition or integrtion. If F(x) is continuous on nd F (x) f (x), for ll x (,b), then F is clled n nti-derivtive of f. Anti-derivtives indefinite integrls Definition 5. This chpter is devoted to integrtion concepts nd its techniques. Techniques of Integrtion Integrtion by Substitution Integrtion by Prts Integrtion by Prtil Frction Trigonometric Integrls Integrtion by Trigonometric Substitution Definite Integrl Fundmentl Theorem of Clculus 5.4 Appliction of Integrtion Are Volume Arc Length Surfce Are Improper Integrl Exercise 37 Integrtion is one of the two min opertions in clculus, with its inverse differentition.
#Zoom math 500 showing steps integrals how to
Let’s look at a few examples of how to apply these rules.1 Chpter 5 Integrtion Contents 5. Recall the integration formulas given in the table in Antiderivatives and the rule on properties of definite integrals.
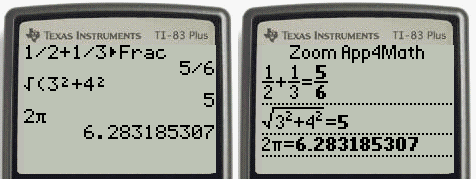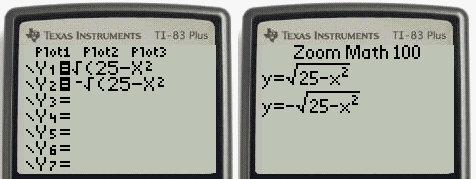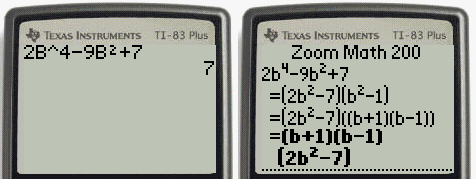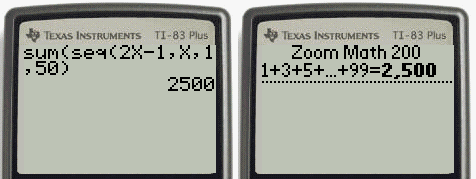


However, until these concepts are cemented in your mind, think carefully about whether you need a definite integral or an indefinite integral and make sure you are using the proper notation based on your choice. You will naturally select the correct approach for a given problem without thinking too much about it. As you become more familiar with integration, you will get a feel for when to use definite integrals and when to use indefinite integrals. An indefinite integral represents a family of functions, all of which differ by a constant. A definite integral is either a number (when the limits of integration are constants) or a single function (when one or both of the limits of integration are variables). Although definite and indefinite integrals are closely related, there are some key differences to keep in mind. It is important to note that these formulas are presented in terms of indefinite integrals. In this section, we use some basic integration formulas studied previously to solve some key applied problems. 5.4.4 Apply the integrals of odd and even functions.5.4.3 Use the net change theorem to solve applied problems.5.4.2 Explain the significance of the net change theorem.5.4.1 Apply the basic integration formulas.


 0 kommentar(er)
0 kommentar(er)
